量子テレポーテーションをQiskitでもやってみる

　量子テレポーテーションに関しては、これまでに何度か記事を書きました。例えば次のようなものです:

・超高密度符号化と量子テレポーテーション（その３）

・Reconfirmation of quantum teleportation using Qni

　これらの記事では、主に量子回路シミュレータQniを使って、説明してきました。内容はほぼ同じなのですが、今回は、Qiskitを使ってみました。新たに分かったこともあるので、記録しておきたいと思った次第です。

地球と月の間の量子テレポーテーション

●量子ビットと古典ビットの並び順の相違

　これは（Qiskitに限らず）混乱しやすいので、改めて図１にまとめた。（本図は、私のオリジナル作品）まず、複数の量子ビットシステムのテンソル積での並び順であるが、量子回路図では、これを右側に起こして直立させたものになる。次に、これらの量子ビットの測定結果（古典ビット列）の並び順は、これを右側へ倒して水平にしたものと対応する。すなわち、テンソル積と古典ビット列では、上位と下位が逆転する。これは、慣例となっているので、注意する必要がある。図３にもこれが表れる。

●量子テレポーテーションで転送したい量子ビット状態の設定

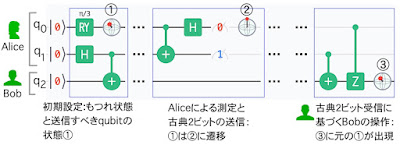
　任意の量子ビット状態を転送できるのだが、ここでは、一例として、図２に示す量子状態とする。すなわち、量子ビット|0>に対して、Y軸周りに60°回転、さらにZ軸周りに60°回転させた状態を設定した。

　QiskitではComposerとQuantum Labの２つが使える。どちらでも、量子状態ベクトルを表示できる。何か詳細な設定が必要であれば、上図のように、Quantum Labでコーディングすることができる。もちろん、次の図３と同じ量子回路図も、Quantum Labで書くこともできる。

●量子テレポーテーションをQiskit Composerでシミュレートする

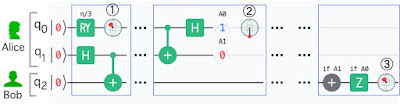
　さて、ここからが本論なのであるが、原理的なことはすでに上記ブログ記事に十分書いているので、重複する部分は省略する。図3は、図２で設定した量子ビット状態を、AlcieからBobへ転送する様子である。下段には、Aliceの測定結果としての古典2ビット情報の発生確率と、AliceとBobの３量子ビットシステムの確率振幅が表示されている。

　この図で最も重要な点は、Aliceの量子ビット状態①が、Bobの量子ビットに設定されることである。つまり、①と⑥は全く同一の状態である。しかし、①の状態はすでに消滅して⑦のようになっている。これは量子複製不可定理に則っていることなのである。

　すでに既報では、Aliceが②で測定を行う直前の状態は、４通りあり、それぞれ1/4の確率で発生することを示した。図下段の③からそのことが確認できる。これは、Composerが自動的に②の測定を1024回実行（shot）した結果なのである。つまり、測定結果の古典ビット列000、001、010、011の出現確率がそれぞれほぼ等しく、25%程度となっており、それらの合計は100%であることが実証された。なお、３ビットの並びの最上位は0となっているが、これは、Bobの量子ビットがこの時点では測定されていないことによる。また、②の測定の直前に、Aliceが自分の２量子ビットに逆Bell回路を適用していることにも注意する。

　最後に、右端の３量子ビットシステムの状態をみてみよう。この例では、②の測定結果が10であり、|q[2]>|1>|0>という状態になっている。測定結果によらず、q[2]の状態は必ず⑥（すなわち①）となる。そうなるように、Bobによる④の操作（制御付き量子ゲート）が設定されているのである。q[2]が|1>となる確率が0.25（|0>となる確率は0.75）であることは図２に示したので、⑤の確率振幅の分布は納得できるであろう。

●Qiskit Composerのその他の機能

　図３の②での一回の測定結果として、特定の２ビットパタンが必要な場合は、図４上部のVisualizations seedを変更して試すことができる。また、図中の量子ビット状態を示す円盤には、量子ビットのpurity（量子もつれの有無）を示す情報も含まれるので、量子回路の検証に利用することができるだろう。

Reconfirmation of quantum teleportation using Qni

Quantum teleportation has already been covered in detail in this article. This time, I would like to reconfirm the point by executing it with the quantum circuit simulator Qni.

In the previous article, Bob applied his I-, X-, Z-, and Y-gates to his qubits, corresponding to the classical 2-bit information 00, 01, 10, and 11 received from Alice. This allowed Bob to obtain the state of the qubit sent by Alice. Logically this is fine. However, when running on the Qni, I found it easier to apply the X and Z gates in succession instead of the Y gate. The description will be made accordingly.

(1) Use of CX (Controlled X) and CZ (Controlled Z)

Considering the gate that Bob should apply to his qubit according to 00, 01, 10, 11 mentioned above, we arrive at the following simple conclusion [3]:

  step1: If the lower bit of the received 2-bit information is 1, the X gate is applied.

  step2: If the upper bit of the received 2-bit information is 1, the Z gate is applied.

According to this, the CX gate and CZ gate can be applied as follows. Note that either |0> or |1> is input to the CX and CZ control lines (other qubits are not input).

As an example in the above diagram, ① is set with the RX(π/3) gate, but any state is acceptable. There are two points worth noting here. First, the state of qubit ① that Alice wants to send to Bob vanishes in Alice's measurement shown in the center, resulting in ②. Nevertheless, the state of ① appeared in ③ by applying the gate by Bob shown on the far right. It matches the No Cloning Theorem. This is exactly what quantum teleportation is.

Second, regardless of the measurement results (classical 2-bit information) by Alice in the central part of the figure, Bob on the far right only needs to apply CX and CZ continuously. However, when Bob is far away from Alice, it is difficult for us to imagine Bob receiving classical 2-bit information from Alice through normal communication. To clarify the image, the following alternative (explicitly checking the classical bits) can also be used.

(2) Explicitly examine classical 2-bit information and apply necessary gates

In Qiskit, etc., classical bit registers can be referenced, but in Qni, the corresponding processing can be realized by adding an execution condition (if) to the gate as shown in the figure below.

In this example, since the measurement result by Alice in the center of the figure is "10", it can be seen that the X gate applied by Bob does not work (it is dark) and only the Z gate is applied.

In this article, I referred to [1] for the principle and mechanism of quantum teleportation, [2] for the Qni simulation, and [3] for the Qiskit simulation.

References

[1] Chris Bernhardt, “Quantum Computing for Everyone”, MIT Press, 2020

https://www.chrisbernhardt.info/

[2] Qni; https://github.com/qniapp/qni

[3] Satoyuki Tsukano, "Inside the mind of a quantum computer", Gijutsu-hyoron-sha, June 2023. (in Japanese)