「量子コンピューティングを学ぶ」をある会誌に寄稿

　量子コンピューティングに関する私のブログ記事は60件を超えました。ここからご覧いただくことができます。

　ところで、情報処理学会誌の最新号に、根本香絵氏による量子コンピューティングに関係する解説（全６ページ）[1]が掲載されています。一般向けの啓蒙、解説記事として、とても分かりやすく、有用だと思います。実は、同じく６ページで、私は同様の独自解説的記事をある機関の会誌に寄稿していました。残念ながら、その会誌は（数千人の会員限定であり）一般には非公開であるため、ここで参照できません。しかし、私の記事の原稿は以下に置いてありますので、よろしければご覧ください。

「量子コンピューティングを学ぶ」

https://drive.google.com/file/d/1r2sWnstCrcOnikB0QdYeqoxM66YVF1BS/view?usp=sharing

　どちらかというと「量子コンピューティングの基礎をどのように学んだのか」を主に叙述しています。具体的な内容は、参考文献[2]で学んだことに基づいています。上記の物理学者根本氏とは異なる切り口で書いていますので、読み比べて戴くのもよろしいかも知れません。

June flower, hydrangea (紫陽花), Atsugi

Rice planting season (田植え) has come again this year, Atsugi

How did I learn the basics of quantum computation in half a year from zero knowledge? In response, I wrote about my encounter with Prof. Chris Bernhardt's book, which led me to various amazing quantum algorithms, and my experience using the Hitachi CMOS annealing machine and the IBM Quantum machine.

If I were to compare it to the plan to climb Mount Everest, it would be the feeling of finally leaving for base camp. I would appreciate it if you could refer to something. (The article was written in Japanese, but you might use automatic translation if you need it.)

参考文献

[1] 根本香絵,"2022年ノーベル物理学賞に 量子もつれと量子情報科学", 情報処理 Vol.64 No.7 July 2023, pp.320-325

[2] Chris Bernhardt: Quantum Computing for Everyone, The MIT Press, 2020.

https://www.chrisbernhardt.info/

愛読書に手製のブックカバーを取り付ける

　何度も繰り返して読んだ（学んだ）量子コンピューティングに関する英語書籍（ペーパーバック装丁）があります。マーキング、線引き、書き込み（消しゴムで取消しも）、メモ用紙の挿入などもしながら、見開きを重ねた結果、綴じ部分のほつれや、表紙の圧着ビニールの剥離が少し出てきました。

　今後も何度も参照するので、今のうちにカバーを取り付けたいと思いAmazonで探しましたが、このサイズに適当なものが見つかりません。文庫本や新書版のブックカバーはたくさんあるのですが。そこで、自作することになりました。厚手の大きめの紙を折り曲げて作るのです。

　ただし、無地では淋しい。納得できるデザインや模様が入っている紙が欲しい。あれこれ選んで決めたのが以下の３種類です。

1. 通販で見つけたパリの古地図が印刷されたクラフト紙
2. 贈答用の高級カステラの箱の包装紙
3. ロンドン市街地図（1987年8月英国出張時に購入、古いがカラーで綺麗）

　ブックカバーをそのまま取り付けると、原書の表紙のデザインが分からなくなります。そこでポイントは、小さな窓をくり抜くこと。その後ろから、webサイトに掲載されている書籍のサムネール画像を貼り付けるのです。さらに、背表紙にもタイトルを切り抜いて貼り付けます。

　３種類も作ったので、その時々の気分で適宜着せ替えれば良い。末長く役立つ愛読書にふさわしいブックカバーができた！

生成AIブロックがMIT App Inventorで使えるようになった(1)

　昨日（2023-06-20）、MIT App Inventor version nb193がリリースされ、新たに生成AI系ブロックが使えるようになった。すなわち、ChatGPTとDALL-E2を利用するChatBotとImageBotである。早速、簡単な例を考えて試してみた。なかなか素晴らしい！応用はまだまだこれからだろうが。（→続編はこちら）

●私の考えた簡単な質問：

「次の５つの行動からランダムに一つを選んでください:

learn quantum mechanics, lecture in front of students, climb Mt. Fuji, shake your dice, swim in the sea」

●ChatBotとImageBotの答え：

質問に答えて、どれかを（例えばshake your dice）選んで、そのイメージを図示してくれます！

　普通のアプリでは、行動リストの中からランダムに選ぶコードも書きます。しかし、ここでは、そのコードは書かずに、ChatGPTが指図を理解して選択しています。ここにも、生成AIの片鱗を窺えるのです。

　こんな風に楽しんでいると、なんと、OpenAIの無料枠API利用回数限度に達して使えなくなってしまった。だが、24時間後にはリセットされて、1日あたり数十回はリクエストできるようだ。それを超える場合は、有料プランの契約が必要。

[追加]他にもなかなかの結果がありますので、追加します。

　"harvest cabbage（キャベツを収穫）"と、"teach math（数学を教える）"です。それらしい雰囲気が出ています。Very goodですね。

　もう２つ行きます。２つの行動を同時に選んで、そのイメージを描いてもらいました！

"climb Mt. Fuji, teach math"(富士山にのぼり、数学を教える)と"swim in the sea and harvest cabbage" (海で泳ぎ、キャベツを収穫する)です。なかなか創作力ありますわ。

MIT App Inventor version nb193:

https://community.appinventor.mit.edu/t/mit-app-inventor-version-nb193/87279

A mobile app that simulates the Ekert protocol for quantum key distribution

Abstract: In my previous article, I theoretically described how the quantum key distribution protocol Ekert, which uses streams of entangled qubit pairs, works, referring to [1]. This time, for each individual qubit, an orthonormal basis is randomly chosen and the measurements are simulated. As a result, confirm that the same conclusion (probability value) as the theory is obtained. A mobile application for this purpose was developed using MIT App Inventor. By creating such an app, we can deepen our understanding of measurements involving quantum entanglement.

●What can you do with the mobile app?
The app logo, shown in Fig. 1, highlights the features of this mobile app. Now the pair of qubits possessed by Alice and Bob are in an entangled state, and they measure each other on different orthonormal bases (hereafter simply called bases). There are three types of bases that can be selected. Without eavesdropping, the probability that both measurements agree is 1/4. If there is eavesdropping, the probability increases to 3/8. This app can verify these theoretical values for a large number of entangled quantum pairs (eg, 3000 pairs).

●Run the mobile app to validate the Ekert protocol
Fig.2 shows an execution example of this application. (a) is the case without wiretapping. First Alice makes the measurements, then Bob makes the measurements. Since the qubit pairs are in entangled states, Bob's measurement depends on Alice's measurement. The theoretical value of the matching probability between the two measurement results is 1/4 (=0.250), but the execution result of this application was 0.254. I'd say it's an almost perfect match.

On the other hand, in the case of eavesdropping, the situation is as shown in Fig.2(b). Suppose Eve has eavesdropped (namely measured) a qubit before Alice and Bob. Alice then measures. It depends on Eve's measurements. After that, when Bob measures, it depends on Eve's, but not on Alice's. This is because the entangled states between qubits have disappeared when Eve measures them. The matching probability between Alice and Bob's measurement results is theoretically 3/8 (0.375), but the application execution result is 0.374. This was also an almost perfect match.

From the above observations, we can say that this app simulates the Ekert protocol correctly. If it is confirmed that there is no eavesdropping as in FIg.2(a), the measurement results of 1001 pairs, which is about one-third of the 3000 pairs, can be shared as a secure quantum key. A great advantage is that there is no need to exchange the key between the two, that is, there is no need to send it to each other. In fact, in this case, ["a",1]["b",1]["b",1]["b",0]["a",0]["c",0]["b",1]["a",1]["a",1]["c",0]["a",1]["a",0] ... match both, so the classical bit string "111000111010..." can be an encryption key.

●Mechanism of the mobile app
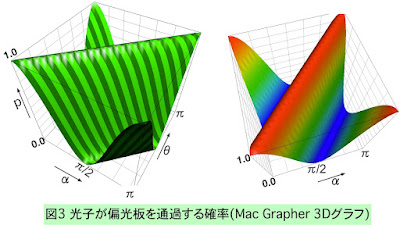
The most important parts of this mobile app are shown in Fig.3. This deals with the cases where the results of measuring  qubits by the base ① are the classical bits shown in ②. The probability ④ that results in "|0>" when measuring such a qubit with a newly selected basis ③ is stored in the table on the right side of the figure. From such information, we can obtain the result (classical bit) of measuring the qubit by the basis of ③.

Note that this measuring block that uses the photon transit probability can also be constructed as shown in the figure below, without using a table:

●Additional information

This app uses random numbers, so the results will vary slightly each time you run it. However, I would like to confirm that this is not an obstacle in determining the presence or absence of eavesdropping. FIG. 4 shows the results of 25 runs of the 3000-pair entangled quanta measurements shown above. Fig. 4(a) shows the probability that Alice's and Bob's measurement results agree with each other (when they choose different orthonormal bases) both with and without eavesdropping. Both probabilities were found to be in good agreement with the theoretical values (0.375 and 0.250). On the other hand, Fig. 4(b) shows that the quantum key length that can be used when it turns out that there is no eavesdropping agrees well with the theoretical value (here, 1,000).

In the above, the length of the quantum pair is assumed to be 3,000. Fig.5 shows the results when this length is changed to 150 and 30,000. With a length of 150, it is difficult to determine the presence or absence of eavesdropping. On the other hand, when the length is set to 30,000, it was found that the presence/absence of eavesdropping can be determined more clearly than in the case of Fig.4.

----------------------------------------------------------------------------------

My recent quantum computing related mobile apps : Polarization, the BB84, and the Ekert. Both were developed based on Reference[1].

----------------------------------------------------------------------------------

Reference

[1] Chris Bernhardt: Quantum Computing for Everyone, The MIT Press, 2020.

https://www.chrisbernhardt.info/

Detecting eavesdropping in Ekert protocol for quantum key distribution

Abstract: The Ekert protocol is a secure key distribution protocol that utilizes a stream of two qubit pairs in an entangled state. Alice and Bob each measure the received quanta using a randomly chosen orthonormal basis. The degree of matching between the classical bit strings of the two as a result indicates the presence or absence of eavesdropping. This is explained in the last section of chapter 8 "Bell's Inequality" of reference [1]. There, the calculation of the match probability in the absence of eavesdropping is clearly explained. However, details of how to calculate the matching probability (=3/8) in the case of eavesdropping are not shown. This blog post tracked that calculation.

●Primitive cryptographic key distribution using quantum entanglement
Quantum entanglement makes it possible to share cryptographic keys without having to create them in advance and send them to each other. However, as shown in Fig.1, in practice, such a method cannot be used easily. This is because, if eavesdropped, it cannot be detected.

●Ekert protocol (E91) for quantum key distribution

The solution is the Ekert protocol. Send a stream of entangled pairs of qubits (of length 3n) to Alice and Bob. They receive the qubits one by one from the pair. Each time, they both randomly select one of the three orthonormal bases to measure one's qubit. The results of the measurements are recorded along with the basis of choice. Finally, both sides exchange selected bases information (not measurements) in normal communication. Of these, approximately n bases should be the same in both, and the remaining 2n should be different in both.

For bases (2n of their own) that do not agree between them, they exchange their measurement results. It can be done by normal communication without encryption. When calculating the probability that the measurement results match, the value becomes 1/4, if there is no eavesdropping by a third party (that is, if the third party does not measure the qubits). Details of the calculation are given in reference [1]. If the value can be confirmed, the measurement results for the remaining n bases that agree with each other can be used as  an encryption key. That is, both parties can share the encryption key without sending it to each other. See Fig.2(1).

However, if a third party Eve eavesdrops on the qubits before Alice's and Bob's measurements, the matching probability of Alice's and Bob's measurements changes to a value of 3/8. See Fig.2(2). But how is this value calculated? I will clarify that next.

●Comparison of Alice's and Bob's measurement results when eavesdropped
Fig.3 shows the calculation of the match probability (3/8) mentioned above. See diagram for details. There are nine combinations of bases that Alice and Bob can choose from, but we are only interested in the cases that their bases are different. The match probability for the six combinations is shown in red. In this example, Eve chose Standard basis, but she would have chosen anything else.

Fig. 4 shows in more detail the calculations for cases (a) and (b) among the six combinations. Eve's results are measured by Alice and Bob on the basis of their choice. The probability amplitude at that time is used in the calculation.

From the above, the Ekert protocol mechanism for generating cryptographic keys and detecting eavesdropping by a third party has been completely clarified.

Special Acknowledgment

I have forwarded this blog post to Prof. Chris Bernhardt, the author of reference [1]. He sent me an email confirming that this calculation is correct. Below is the last two lines of his answer. I would like to thank him. (2023-06-12)

Reference

[1] Chris Bernhardt: Quantum Computing for Everyone, The MIT Press, 2020.

https://www.chrisbernhardt.info/

Confirmation of quantum key distribution protocol BB84 with smartphone app (supplement)

[Abstract] BB84 (quantum key distribution protocol) is excellent among the limited applications when using a single qubit (that is, not using quantum entanglement). I've written an article about this in the past, but I'll add it here to make it even clearer. This BB84 is also a good example for learning "measurement of quantum states by orthonormal basis".

●What is BB84 (reconfirmation)
BB84 is a method in which 1/4 of Alice's classical bit string of length 4n is used as a secure key between them without sending it directly to Bob. Alice randomly selects an orthonormal basis for each bit of the classical bit string of length 4n, and sends the basis vector (quantum state vector) corresponding to that bit to Bob. Importantly, a method is included to determine if this transmission has been intercepted by a third party, Eve.

●Blog articles written in the past
I wrote the BB84 method in detail in the blog post below. (The figure is also reproduced.)
https://sparse-dense.blogspot.com/2022/11/bb84.html

Now, when I read it again, I didn't find any particular mistakes, but I felt that the explanation was a little lacking, so I added the following section "How to actually configure the BB84".

----------（Supplementary explanation added）----------------------------
●How to actually configure the BB84
The theory is now explained. From the above explanation, the number of times Alice and Bob's chosen bases match is 2n. The resulting bit string measured by Bob on that matched base matches the bitstring Alice has. So, assuming no eavesdropping, Alice does not send the 2n long bit string to Bob and they can both share the bit string as a key.

However, in reality, Alice is sending the basis quantum state vector to Bob, so we have to check whether it is wiretapped. Therefore, both parties send each other n-length bit strings, which is half of this 2n-length bit string, by "unencrypted normal communication" and confirm the degree of matching. If they match perfectly, it can be said that there is no eavesdropping. On the other hand, if 1/4 of them do not match, it can be said that there was wiretapping. (It takes advantage of the fact that eavesdropping requires measuring its qubit (quantum state vector), which changes the quantum state to be sent to Bob.)

If we find no eavesdropping, we can safely use the other half of the matched 2n long bit string as the key. (Actually, 2n lengths match, but half of them may be known to others due to the above-mentioned normal communication.)

---------------------------------------------------------------------

A smartphone app reproducing the appearance through polarizers

Abstract

This app shows what it looks like with some polarizers placed between the image and the eye. That is, the polarization angle of the photons emitted from the plane of the image and the axis angles of the polarizers are used to calculate how bright they appear. The mathematical model is fully explained in Prof. Chris Berhardt's book "Quantum Computing for Everyone". This relates the spin of an electron to the polarization of  a photon.

■ Experiments on light using polarizers

A typical experiment is shown in Fig1. When a polarizer with an axis angle of 0° (north direction) is superimposed on another polarizer with an axis angle of 90°, it becomes completely dark as shown in (a). This is because no photons pass through the second polarizer due to the fact that the two directions are perpendicular. However, when a polarizer with an axial angle of 45° is inserted between these two polarizers, the image can be seen to some extent well as shown in (b).

■ A smartphone app that simulates polarizers

We designed a smartphone app that can perfectly reproduce the above mysterious phenomenon, and developed it quickly using MIT App Inventor. Fig.2(a) shows its user interface. On the other hand, Fig.2(b) is the explanation screen of the mathematical model which is the principle of this application. This shows the formula for calculating the probability of a photon passing through a polarizer. This probability is reflected in the transparency of the color. Furthermore, Fig. 3 shows it visually.

The experiments with this app shown in Fig.4(a) and Fig.4(b) correspond to Fig.1(a) and Fig.1(b), respectively. The axis angle of each polarizer can be set with a slider. These results perfectly reproduce the manual experiments shown in Fig. 1(a) and (b). And Fig. 5 shows the observation when the polarization angle θ of the incident photon is changed from 0° to 45°. This result also seems perfectly convincing.

■ Youtube video showing how this app works

The above experiment using this app is published in the following Youtube video:

https://youtu.be/wGJEK0RhXkA

(the link to the video has been updated, so please click again.)

■ MIT App Inventor program

As mentioned above, this app was efficiently developed with MIT App Inventor. Fig.6 shows its main part. The polarization angle of the incident photon and the angle of the axis of the polarizer determine the probability of the photon passing through it, and determine the color transparency accordingly.

■ A little improvement for your enjoyment

You can also change the background image and user interface design to your liking. Fig.7 shows an example.

光子が偏光板を通過する確率のグラフ表示

[要旨] 偏光板の重ね合わせで起こる不思議な現象を再現するスマホアプリを前回作成しました。そこでの要点は、量子重ね合わせの原理に基づき、光子が偏光板を通過する確率を計算することでした。今回は、単にそのビジュアライゼーションに過ぎませんが、2D、3Dグラフ表示で通過確率の様子を楽しみます。

■光子が偏光板を通過する確率のグラフ表示
　偏光角度θの光子が軸角度αの偏光板に到達した場合、光子がそこを通過する確率pは、量子計算の基礎事項にも基づき以下のように計算できます。

p = (cosθcosα + sinθsinα)の平方

　この確率pを3Dグラフ表示したのが図１です。ちょっとたいそうなグラフになってしまいました。角度θとαが等しい場合だけ確率p = 1.0（最大値）となり、両者が直交する場合はp = 0.0（底面の最小値）となることが確認できます。また、全体としては、対角線に直交して進むsin波のようになっています。

　さらにもう少し分かりやすくするため、光子の偏光θの軸でスライスして、2Dグラフ表示したものが図２です。

　

　ついでに、Mac Grapherによる、方程式からのグラフ描画も載せておきます。

量子力学計算に基づいて偏光板を模擬するスマホアプリ

[要旨] 偏光板の重ね合わせで起こる不思議な現象は、量子コンピューティングの数学モデルによって、すでに説明がついている。→こちらと→こちらにその記事を書いた。今回の記事では、その原理に基づいて開発したスマホアプリ（with MIT App Inventor）について述べる。実物の偏光板で行ったのとほぼ完全に同じ結果を得ることができた。

→その後の改訂版はこちらです。

■スマホアプリの概要
　今回のスマホアプリの外観は図１のようである。動作原理は、既報と同じなので詳細は略す。要点は、ある偏光板に到達した光子の偏光角度がθで、その偏光板の軸角度がαである場合、光子がそこを通過する確率を計算できることである。αとθが等しい場合は通過確率 = 1.0、両者が直交する場合は通過確率 = 0.0 となる。
　スマホ画面での見え方は、偏光板に相当する円盤の塗りの透明度を、その通過確率を適用して調整すれば良いのである。実際の偏光板は正方形が多いが、ここでは、回転処理を簡単にするため円形を用いた。その円盤の回転を明示するため、スライダーを用いて、中心から円周に至る１本の直線を回転させた。 
　なお、最初の偏光板１に到達する光子の偏光角度は全くランダムなのであるが、ここではそれを何らかのフィルターを通して、ある偏光角度になっていると仮定する。一例として、偏光板１に到達する光子はデフォルトでは45°に偏光しているが、ランダムな角度に設定することもできる。

■スマホアプリの実行例
　３枚の偏光板を使う操作例を図２に示す。以下の手順で観察する。

1. 画像に１枚目の偏光板を置くため、偏光板１にチェックをつける。軸角度は0°になっており、この方向に偏光した光子だけが通過するので少し暗くなる。（上記仮定から、光子の通過確率は0.5となるためである。）
2. 次に、一番手前の偏光板３にもチェックをつけて、偏光板３を重ねた状態にする。偏光板３のスライダーを右へ動かすと段々暗くなる。軸角度90°では光子は全く通らなくなり、真っ暗になってしまう。
3. さらに、偏光板1と偏光板３の間に入れる偏光板2にもチェックをつける。そして、その偏光板２のスライダーを右へ動すと段々見えてくる。軸角度45°の時が一番よく見える！この場合、偏光板１を通過した光子が偏光板３も通過する確率は、下図右側の通り、0.25となり、ある程度が画像が見えてくる。

　この操作例はYoutubeビデオとしてここに公開しているので、ご覧いただきたい。

■感 想
　光子がどのように種々の軸角度の偏光板を通過するか（あるいは吸収されるか）は、量子力学計算で明らかにできる。それを、これまでに、机上計算、IBM Quantum実機、今回のスマホアプリの３通りで実現できた。量子コンピューティングの最も基本的な概念の一部の理解を深めるのに非常に有効だと感じた。

　今回のアプリは、MIT App Inventorを用いて、着想から半日程度で実装することができた。（ただし、ユーザインタフェースはその後も手直しはした。）この経験から、「実感する科学」「身の回りの数学」「セミナー」などの題材検討にご参考になれば幸いである。

量子コンピューティングEXPO(2023春)に参加

【要旨】 5/10-12に東京ビックサイトで開催された、量子コンピューティングEXPO(2023春)に参加した。これ以外に、AI・人工知能EXPO、ブロックチェーンEXPO、デジタル人材育成支援EXPOも同時開催されたこともあり、非常に多くの参加者が見られた。本記事では、「量子コンピューティング」についてのみ、簡単に報告する。

■量子ゲート型 vs 量子アニーリング型について

　量子ゲート型に関しては、IBMが1121量子ビットの「IBM Quantum Condor」を発表すると宣言している。また国内では理研から国産初の64量子ビットコンピュータが既に公開された。それでもなお、まだまだ、真の実用化に向けた課題は山積しており、実用問題での確実な成果を見通せる段階ではない。今回のEXPOでもそういう雰囲気があった。一方、量子アニーリング型の方は、各メーカが大学等と共同研究で、実用的な最適化問題（物流、金融、配置、等々）で成果を上げている潮流を感じた。

■大関真之 東北大学教授の量子アニーリングに関する講演

　講演タイトルは、「ビジネススケールに対峙する量子コンピューティング技術」であった。聴衆は恐らく1,000名を超え、"満員御礼"となっていた。彼は、元々、量子アニーリングの創始者である西森秀稔東工大教授のグループで研究した人であり、東北大学へ行ってからは、スタートアップ企業(株)シグマアイを起こした。それだけに、ほとんど、量子アニーリング技術の実世界への適用と今後の見通しであった。現時点では、実用的には、"量子コンピュータ" は、"量子アニーリング型" なのかも知れない。

　(株)高速、という企業の倉庫内の物品（主にトレー）配置最適化への取組みが印象的であった。スーパー等で必要なトレーの種類は多彩である。用途（肉、魚、野菜等々）、大小、形状、デザイン等々で異なる。倉庫には膨大な個数がストックされており、注文に応じてピッキングするのだが、種別の配置が大きな問題である。定常的に数多く出荷されるもの、何種類かがペアで出荷されるもの等があるので、倉庫内にどのように配置すればピッキング効率が上がるか、という問題である。

　この問題は、原理的にはペアの組み合わせ他を考慮すると実に17!（=3兆）個に上るという。もちろん、現場の作業員が長年の経験から、ある程度良い配置をすで行っているのだが、それは数値化されていないし、最適解にどれだけ近いかも分からない。そこに、量子アニーリングの出番がきた。泥臭い地道な検討に多くに時間をかけたが、結論から言うと、現状の配置に対して、人員や作業時間などのトータルコストで、10%の改善を達成できたという。10％と言う数値は素人には小さいな値のように見えるが、大量の物品を日常的に扱う大規模倉庫業においては、非常に価値のある効果なのである。

　一般的に言って、実用的な数理最適化問題においては、古典コンピュータ上での王者とも言えるGurobiに、大規模問題では負ける傾向があった。しかし、ごく最近の取り組み（量子アニーリングと古典数理アルゴリズムの組み合わせ）によって、大規模問題でもGurobiに勝つ見通しを得たという。それは、非常に多くの制約条件の変換を含む、シグマアイのOpt Operationという方式のようである。

■(株)長大のクオンタムシティ構想

　量子技術で都市全体を最適化する、社会を変える、という構想を展示していた。量子技術によるエレルギーや交通などの分野別の最適化だけでなく、分野横断的な最適化を行い都市全体の最適化を目指す。現在の具体的なターゲットしては、配送車、配送ドローンなどの運用最適化であり、そこに、量子アニーリングによる最適化技術を組み入れる。もちろん、官公庁、物流企業、量子コンピュータメーカとの連携体制を強調していた。

■北川勝浩教授（大阪大学）が語る量子コンピュータが導く未来

　これは、会場で配布された「量子ICTフォーラム通信 No.4, 2023」に掲載されているものである。一般には出回っていないので、これを入手できただけでも、このEXPOに参加した価値があった。特集「量子コンピュータが導く2050年の未来 - 誤りのない量子コンピュータで地球規模の課題に根本的な解決策を」として、北川教授が深い思いを語っておられる。

　これを読むと、「量子コンピュータは古典コンピュータよりもどれだけ高速なのか」とか、「日本の量子コンピュータ技術は、IBMやGoolgeに大きく遅れをとっているのではないか」という言い方は、愚問とまでは言えないが、ほとんどナンセンスだと思うようになる。大きな構想を持って、しっかりとした目標を据え、着実に進めていくという腰を据えた取組みこそが価値のあるのだ、そう思うようになる。

　具体的な（ゲート型）量子コンピュータの方式は、まだ誰も、これだと決められる状況ではない。したがって、超伝導方式、イオントラップ方式、光量子方式、半導体方式、中性原子方式の５つを並行して進めている。そうすることで、また別の新たな方式が浮かび上がるかも知れない。東大、日立製作所、大阪大学、日電、理研、慶應大学などがそれぞれを鋭意研究開発している。新進気鋭の研究者たちを励まし、互いに助け合いながら切磋琢磨できるフィールド作りを非常に重視している。こうした北川教授の語りに感銘を受けた。

■感 想

　私の興味は、現時点では、量子アニーリングよりも量子ゲート型に向かっている。しかし、現実的な組み合わせ最適化問題を解く場合は、量子アニーリングをもっと研究し活用すべきだと感じる。

　ゲート型の量子コンピュータについて言えば、今後生き残るハードウェア方式は変わるかも知れないが、量子コンピューティングの数学モデルは量子原理そのものに基づいているので、普遍的なものだと思う。なので、今、その基礎を学ぶのは必然だろう。

　古典コンピュータで非常に性能良くできていることはそのままで良い。そうではない、未解決の、新しい問題に対処するために量子コンピュータがある。だんだん、そういう思いが強くなってきた。そこには、全く新しい世界がある。だから興味が持てる。

　次に予定されているイベントで、私が参加したいと思っているのは、Q2B23 Tokyo（2023年７月）である。多分参加する。

---------------

[蛇足] ChatGPTは感想文は書けない

私：上記の文章を読んだあなたの感想を書いて下さい。要約ではなく。

ChatGPT: 申し訳ありませんが、私は感情を持つことができない機械学習モデルです。私は人間の言語処理を支援するために設計されており、専門的な知識や情報の提供をすることができますが、感情を持つことはできません。