プログラミング例題（ハミルトン閉路問題）：Android版+RNN学習

   【what is this】小規模（５ノード）の有向ハミルトン閉路問題を、前回はマイクロビット（micro:bit）単体で解きました。今回は、それをAndroidスマホで実現しました。MIT App Inventorを用いて、チェックボックスによる接続指定や矢印付きグラフの描画も含めて見やくしました。さらに、Deep Learning（RNN(LSTM)）を用いて、グラフとそのハミルトン閉路の個数の対を、多数学習させる実験も行いました。

■MIT App Inventorを用いたハミルトン閉路解法アプリ
　micro:bit単体では、出力表示が5x5のLEDに限られますが、Androidスマホを使えば、入出力とも、大幅に改善できます。また、この解法は全パス検索となるのですが、具体的なその方法は（順列生成を含めて）、それほど自明ではありません。ですから、スマホでこの解法アプリを設計製作することは、高校〜大学初級におけるプログラミング題材の候補になるはずです。小生のアイディアを以下にご紹介します。
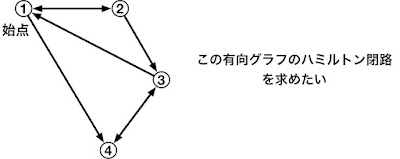
　例えば、以下のような４ノードの有向ハミルトン経路を調べるとします。（目視ですぐに分かるのですが）

　図１(a)のようにして、このアプリで解くことができます。4x4のチェックボックスにチェックを入れることで、ノード間の有向接続を指定します。ボタン"genGraph"によって、それを矢印付きのグラフで表示します。そして、ボタン"solve"を押すと、解が得られます。この例では、解は存在しませんでしたが。

　では次に、ノード数を６に設定して、別のグラフでやってみます。図１(b)の通りです。この例では解は２つ見つかりました。そのうちの一つについては、グラフ上に赤い矢印を付してその経路を明示しています。

■ディープラーニングでハミルトン閉路の個数を学習させる
　次にやってみたのは、「ディープラーニングでハミルトン閉路の個数を発見させる」試みです。５ノードの場合でも、それから作られる有向グラフは、約100万個になります。そのうちの、20万個をランダムに選択します。その各グラフ（接続情報）に対して、上記のような方法で求めたハミルトン閉路の個数をラベルとして付与し、学習させました。図２がその場合の学習データです。

　この学習データをある構造のRNN(LSTM)で学習させた結果を図３に示します。20万件のうち、18万件を学習（訓練）データに、2万件をテストデータとした場合の、テストデータの正解率は、50エポックで99.75%に達しました！
　すなわち、「５ノードのどんな有向グラフを与えても99.7％程度の確率でハミルトン閉路の個数を正答する」ように学習できた、と言えるでしょう。

（注）この学習は、スマホではなく、PCで行いました。

プログラミング例題（ハミルトン閉路問題）：micro:bit版

  【what is this】マイクロビット（micro:bit）のプログラミング例題として、有向グラフのハミルトン閉路問題をやってみました。これは（NP完全問題）であり、効率的な解法は無いようです。そこで、全パス検索になるのですが、DNA（分子生物学の）を使って試験管のなかでこの問題を解いたAdelmanに習い、解の候補となる経路を事前に生成して、それをふるいにかける方式としました。この例題作成をとおして、micro:bitのプログラミングシステムが非常に優れていることを再確認しました。

（⇒本記事の続編はこちらにあります。）

■micro:bitでの有向グラフのハミルトン閉路問題
　micro:bitは最近Version2が発表され、メモリの増強（RAM 8倍化、Flash 2倍化）、タッチセンサやマイク、スピーカーの内蔵などがなされています。今回、これを記念して？ハミルトン閉路問題（始点ノードから出発して、全てのノードを１度だけ訪問し、始点へ戻る経路を探索）を解いてみます。高校生向け講座などの例題になるかも知れません。

　問題設定ですが、micro:bitには、5x5のLED表示しかありませんので、5ノードの有向グラフに限定します。図１のように、ボタンAを押してランダムに５ノード間の接続行列を作るようにします。

　次にボタンBを押すとその解を探索し、見つかった解の個数を表示します。解がなければ0個となります。さらにタッチセンサに触れると、解を電光掲示板方式で１文字づつ流して表示します。これだけですが、ちょっと楽しいプログラミングとなるはずです。

■有向グラフのハミルトン経路問題の解法
　この解法は、全パス検索になります。ただし、AdelmanのDNAを利用した（試験管のなかでの）解法を念頭におき、事前に解の候補をすべて生成します。すなわち、ノード1, 2, 3, 4の順列（4! = 24個しかありませんが）を生成し、その先頭と末尾に0を付加した経路シーケンスが、上で生成した接続行列から作れるかを検査します。出題となる接続行列の個数は約100万個（= 2の20乗）あるのですが、そのいずれに対しても24個の可能性を調べれば良いことになります。ランダムに生成した接続行列では、解が存在しない場合も多く、解があっても、数個程度以内となります。

■micro:bitプログラミング
　この解法のプログラムの主要部を図３に示します。ブロック形式、μPython、JavaScriptの3種が利用できます。ここで特筆すべきは、大まかには最初にブロック形式で作成して、細部をμPythonで作ることができることです。図ではmakePathという関数を作っているのですが、再帰的構造になり、ブロック形式で作成していると細部が考えにくい状況になりました。そこで、μPythonに切り替えて作成するとかなり楽でした。そして、その後、再度ブロック形式に戻ることができるのです！

　さらに素晴らしいと思ったのは、実機のmicro:bitでやる前に、PCでエディタやシュミレータを使えることです。それには、デバッガーやコンソールも使えるという優れた開発環境になっているのです。

■micro:bitは誰のものか？
　micro:bitは、通常、小中高生のプログラミング教育などに広く利用されています。大学ではあまり関心は高くないようです。ですが、上記の経験からも、これは大学でも、初級プログラミングにはかなり使えのではないかと思った次第です。

　micro:bit単体では、確かに作れるアプリに限界があります。しかし、他の機器やスマホとの連動機能も豊富なので、それを使うとかなり高度なアプリも楽しく作れると思います。

■小生がこれまでに作成したmicro:bitアプリもご参考に

　ちょっと手前味噌になりますが、小生がこれまでに、micro:bitと他の機器などと連携させて作成したアプリの情報は以下にあります。ご参考になれば幸いです。

1. Demonstrating Block Chain with a set of micro:bits using radio
2. BBCのmicro:bitで暗号仮想通貨の基礎を知る
3. Consturuct a neural network (multilayer perceptrons) using micro:bit
4. BackPropagation in Neural Network with an Example (XOR) Using Multiple Micro:bits
5. Cooperation between micro:bit and MIT App Inventor with Eddystone signals (No.1)
6. Cooperation between micro:bit and MIT App Inventor with Eddystone signals (No.2)
7. Cooperation between micro:bit and MIT App Inventor (No.3)

⇒本記事の続編はこちらにあります。