光子が偏光板を通過する確率のグラフ表示

[要旨] 偏光板の重ね合わせで起こる不思議な現象を再現するスマホアプリを前回作成しました。そこでの要点は、量子重ね合わせの原理に基づき、光子が偏光板を通過する確率を計算することでした。今回は、単にそのビジュアライゼーションに過ぎませんが、2D、3Dグラフ表示で通過確率の様子を楽しみます。

■光子が偏光板を通過する確率のグラフ表示
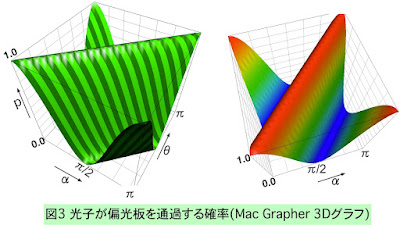
　偏光角度θの光子が軸角度αの偏光板に到達した場合、光子がそこを通過する確率pは、量子計算の基礎事項にも基づき以下のように計算できます。

p = (cosθcosα + sinθsinα)の平方

　この確率pを3Dグラフ表示したのが図１です。ちょっとたいそうなグラフになってしまいました。角度θとαが等しい場合だけ確率p = 1.0（最大値）となり、両者が直交する場合はp = 0.0（底面の最小値）となることが確認できます。また、全体としては、対角線に直交して進むsin波のようになっています。

　さらにもう少し分かりやすくするため、光子の偏光θの軸でスライスして、2Dグラフ表示したものが図２です。

　

　ついでに、Mac Grapherによる、方程式からのグラフ描画も載せておきます。