状態価値関数（ベルマン方程式に基づく）に親しむ（その２）

   【what is this】前回の記事では、ベルマン方程式に基づく「状態価値関数」とは何かをビジュアルに表示して理解しました。そこでは、動き（行動）を決めるための特定の「行動ポリシー」についての状態価値関数を扱ったのですが、今回は、この状態価値関数の値をどの状態においても最大にする（最も優れた）行動ポリシーの自動探索です。

■２次元Grid Worldに対する状態価値関数（復習）
　図１左側の２次元の指定マスから開始して、ひとマスづつ進めて、右下隅のゴールをめざします。移動方向は上下左右ですが、それぞれ選択確率があります。ここでは、右と下へそれぞれ確率0.5で選択され、それ以外は確率0とします。このような行動ポリシーをπRDとします。移動する毎に報酬（-1という負値）が付与されます。各マスからゴールをめざして得られる報酬の合計見込み額が状態価値関数の値です。これは、統計学での「期待値」であり、これが大きいほど少ないステップでゴールします。図1右側の数値は、各マスの状態価値関数値です。ゴールGに比較的近いマスでの値の絶対値は、そこからゴールに至る移動回数と一致しています。

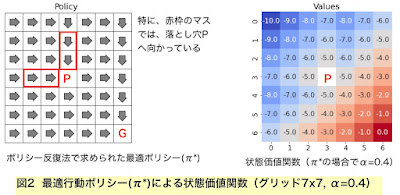
　ここで、中央に「落とし穴P」があることにご注意下さい。移動先がこのPとなる場合は、ただちに、ワープ確率αで左上隅に戻り、確率(1-α)でゴールへ達します。α=0.4の場合は、Pに達すると確率0.6でゴールしてしまうわけですから、Pの回りでの期待値は少し高まるでしょう。実際、例えば、Pの上と左は-6.3となっており、Pが存在しなかった場合の-7.0よりも大きくなっています。

■最適な行動ポリシーを自動的に探索する

　上記では、特定の行動ポリシーπRDについての状態価値関数を示しました。次にやりたいことは、このπRDよりも優れた（大きい状態価値関数値を与える）行動ポリシーを見つけることです。詳細は、参考文献[1]などをご覧いただきたいのですが、その具体的な方法はいくつかあります。ここでは、「ポリシー反復法」と呼ばれるものを使いました。この方法は、簡単に言えば、囲碁の場合でもそうかと思いますが、「一手だけ先読みして最適そうな手をとる」の繰り返しになります。

　ところで、上記の例題の場合、「最適な行動ポリシーπ*」とは具体的にどんなものでしょうか。それは、上記πRDでの確率は0だった左や上方向への行動も含むことになります。そして、「最適」の言葉どおり、各状態（本例ではマス）ごとに、いずれかの方向への移動の確率を１に設定することになります。具体例を図２でご覧下さい。

　落とし穴にP関するワープ確率αの値などは、図１と同じです。図２左側のマスの中の太矢印は、確率１となった行動（移動方向）を示しています。Pの左側と上側の矢印は、積極的に落とし穴Pへ向かっています。これは最適行動ポリシーとして納得できるでしょう。図２右側は、その場合の状態価値関数ですが、こちらも同様に納得できます。

　さらに図３をご覧ください。ワープ確率α=0.1の場合は、もっと高い確率（=0.9）で素早くゴールに達することができるため、Pの広範な周辺のセルからの移動がPに向かっています。これが最適ポリシーになることも理解できます。

　今回の記事はこれでお終いですが、最後に、もっと大きなグリッドで、この技術の素晴らしさを楽しみましょう！美しい図４の結果をご覧下さい。

■まとめ
　分かってしまえば、それほど難しくありません。しかし、「状態の価値」という捕まえ難い概念を、コンピュータで扱えるようにしたこの理論と手法は素晴らしいです。これを最初に編み出した先人に敬意を表したい気持ちになります。さらに、一歩づつ先へ進みたいと思います。また、参考文献[1]の丁寧で精緻な叙述は、学習意欲を維持するのに非常に大きく貢献しています。本記事は、これ基づいて（説明文や図は小生の自作ですが）書きました。

[参考文献]

[1] 中井悦司：ITエンジニアのための強化学習理論入門、技術評論社、2020年７月