I am a professor emeritus of CS at Kanagawa Institute of Technology, Japan. Originally my specialty was parallel and distributed systems. My current interests include machine learning, natural language processing, creating mobile apps with MIT App Inventor, and quantum computing. In the web version of this blog, clicking the icon on the right (a plastic sphere) will take you to the "List of Quantum Computing Articles". - Fujio Yamamoto (for e-mail, add "@ieee.org" after "yamamotof")
YouTubeに「ドル札で折るピラミッド（Dollar Origami Pyramid）」なる動画（下部参照）がありました。良さそうに思い、やってみました。１ドル紙幣以外にも、数種類の長方形の紙で折ってみましたが、なかなかおしゃれな作品となります。古代エジプトピラミッドに比べると、先端がより鋭く尖っているようです。
今回はクイズです。
ある入力データに対する出力結果が図１に示してあります。入力データは、「千山万水」の四字熟語から、ランダムに漢字を選んで次々と並べた、長さ12の文字列です。このような入力データは、約1,700万個（4の12乗個）作れますが、図１にはその一部を示しています。それに対する「ある処理」を行った結果の出力データが右側に示されています。
私は、このようなどの入力データに対しても、（恐らく）100%正しく出力結果を示すことができます。私は、図２のようなヒント（赤字の情報）は一切もらっていません。入力と出力の組みを5万個見て、「その処理」をひたすら学習しただけです。その結果、その処理内容を把握できたことを確信しました！
さて、私は誰でしょうか。人間ではありませんが。
答えは、こちらの記事にあります。
（入力データのボキャビュラリが、「A,T,G,C」から「千,山,万,水」に変わっただけなのですが、Attention付きSeq2seqの感動が尾を引いていましたので、こんなクイズ記事になっています。）
【what is this】これまでのIntelプロセッサに替わり、Apple独自のM1(arm64)プロセッサ搭載のMacが発売になっています。Appleシリコン搭載とも呼ばれています。何といっても、「8コアCPU+ 8コアGPU+16コアNeural Engine」と言われると、長年のMacファンとして買わざるを得ませんでした。基本的なソフトウェアのネイティブ本格対応はこれからのようですが、現時点でも、手元の例題で、Intel版に対して、Javaアプリで3.2倍、Pythonアプリで2.5倍高速となりました。今後の、M1向けTensorflow(アルファ版はすでに公開)などが楽しみです。
 |
| 雑然とした「研究室」に置かれた新型M1 Mac mini |
■Javaアプリで試す
小生の使う開発言語は、Java、Python、NetLogo、MIT App Inventorなどです。まず、Javaのアプリで確認します。Androidアプリで扱ったHamilton閉路問題のうち、サイズを少し大きくした、Groetzschグラフ（11ノード）を例題とします。最も原始的な解法なのですが、10ノード（出発は第0番ノードに固定するので）の順列（約360万個）を全て調べるものです。もちろん、可能な限り早期に適合しないパスは棄却します。図１に示すような、Hamilton閉路20個を全て答えます。
このJavaプログラムの主要部（というよりも全体制御部）は、図２のとおりです。並列ストリームを使っています。実行の結果、M1 MacはIntel Macよりも、約3.2倍高速でした。素晴らしい！PC買い換えで３倍超の性能アップは、なかなかないです。
■Pythonアプリで試す
次にPythonアプリです。例題としては、すでに報告しました、ショットガン法によるDNAの復元問題（トイプログラム）です。Deep Learningでのprediction部分です。ここでは、上記Javaのようなparallel機能は特に意識せず、GPUの使用もありません。ですが、CPUのコア数の違いが、図３のとおり、実行性能に現れています。この例でも、M1 MacはIntel Macよりも2.5倍高速でした。
■今後の期待：M1用に最適化されたTensorflow等
以上、現時点で試せるJavaとPythonの例題をM1 Mac miniで実行してみました。従来よりも2.5倍〜3.2倍の高速化となったことは素晴らしいと思います。現時点ですでに、GPUやNeural Engineを駆使するであろうTensorflowのアルファ版は公開されています。今後、それも利用していけば、Deep Learningを手元のマシンで実現できる場面が広がりそうです。
This app has won the "2021 March's MIT APP INVENTOR OF THE MONTH" award.
Abstract
This app solves the Hamiltonian cycle problem for a given graph. The problem is to find out paths in a directed graph of n vertices, starting from one starting point, visiting all vertices only once, and returning to the starting point. This is known as an NP-complete problem and no efficient solution is known in general. From the perspective of programming education, I provide a solution for small graphs with six or fewer vertices, along with an easy-to-use user interface.
Basically, it searches all possible paths, but the method is not so trivial and you need to think carefully about the procedure. The use of multiple lists and recursive functions in implementing the algorithm is useful for improving programming capabilities. You should also consider the graphical user interface for setting up and displaying graphs. The sense of accomplishment gained by completing this app enhances the educational effect. It's also fun to run the finished app and see the results on the graph.
This time, I used MIT App Inventor to create this app. The use of App Inventor's familiar feature blocks (especially Lists, AnyComponent, Canvas, Checkboxes, etc.) was very useful for efficient program development.
●This app is published on the Google Play Store:
https://play.google.com/store/apps/details?id=appinventor.ai_Fujio_YAMAMOTO.HamiltonianCycles1
●The source code of this app is published below :
https://gallery.appinventor.mit.edu/?galleryid=3048beec-25b8-46ba-a746-25c0dc3702b6
Directed graphs and the Hamiltonian cycle
Figure 1 shows an example of a directed graph and the Hamiltonian cycle. A single matrix can be used to represent the connections between nodes. In this matrix, the "From" node is in the row and the "To" node is in the column. In the example, there are two Hamiltonian cycles. This app provides both a way to give a directed graph with such a matrix and a way to automatically generate a random graph.
How to use the app for the Hamiltonian cycle problem
Fig.2 shows the GUI of the app developed this time. The number of nodes can be specified in the range of 2 to 6. If you want to specify a directed graph in the matrix on the left, check the check box "prefer Matrix". After that, when you press the button "genGraph", a graph with an arrow will be drawn on the canvas at the top. Next, if you press the button "solve", the Hamiltonian cycle will be searched, and as a result, the number of cycles and the path of each cycle will be displayed. On the other hand, if you want to generate a graph randomly instead of specifying the graph yourself, uncheck the check box "prefer Matrix". Even then, the matrix corresponding to the generated graph is automatically displayed. It would be fun to discover such a cycle for different graphs.
【what is this】小規模（５ノード）の有向ハミルトン閉路問題を、前回はマイクロビット（micro:bit）単体で解きました。今回は、それをAndroidスマホで実現しました。MIT App Inventorを用いて、チェックボックスによる接続指定や矢印付きグラフの描画も含めて見やくしました。さらに、Deep Learning（RNN(LSTM)）を用いて、グラフとそのハミルトン閉路の個数の対を、多数学習させる実験も行いました。
■MIT App Inventorを用いたハミルトン閉路解法アプリ
micro:bit単体では、出力表示が5x5のLEDに限られますが、Androidスマホを使えば、入出力とも、大幅に改善できます。また、この解法は全パス検索となるのですが、具体的なその方法は（順列生成を含めて）、それほど自明ではありません。ですから、スマホでこの解法アプリを設計製作することは、高校〜大学初級におけるプログラミング題材の候補になるはずです。小生のアイディアを以下にご紹介します。
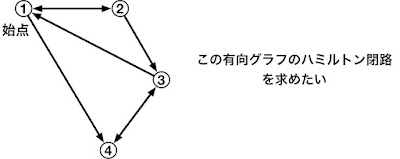
例えば、以下のような４ノードの有向ハミルトン経路を調べるとします。（目視ですぐに分かるのですが）
では次に、ノード数を６に設定して、別のグラフでやってみます。図１(b)の通りです。この例では解は２つ見つかりました。そのうちの一つについては、グラフ上に赤い矢印を付してその経路を明示しています。
■ディープラーニングでハミルトン閉路の個数を学習させる
次にやってみたのは、「ディープラーニングでハミルトン閉路の個数を発見させる」試みです。５ノードの場合でも、それから作られる有向グラフは、約100万個になります。そのうちの、20万個をランダムに選択します。その各グラフ（接続情報）に対して、上記のような方法で求めたハミルトン閉路の個数をラベルとして付与し、学習させました。図２がその場合の学習データです。
この学習データをある構造のRNN(LSTM)で学習させた結果を図３に示します。20万件のうち、18万件を学習（訓練）データに、2万件をテストデータとした場合の、テストデータの正解率は、50エポックで99.75%に達しました！
すなわち、「５ノードのどんな有向グラフを与えても99.7％程度の確率でハミルトン閉路の個数を正答する」ように学習できた、と言えるでしょう。
